티스토리 뷰
확률 구하는 총 세가지 방법
1. 분포의 밑넓이
분포의 밑넓이를 이용하여 확률을 구할 수 있다. 모평균, 표준편차를 이용하여 표준화를 진행한 후에 해당 값을 표준점수로 변경하면 분포의 밑넓이를 구할 수 있다.
2. 표준정규분포표
표준화를 진행하여 구한 표준점수까지의 밑넓이는 표준정규분포표를 보면 바로 구할 수 있다.
3. 표준정규분포표의 특성
표준정규분포표의 특성은 밑넓이가 1이고 좌우대칭이다.
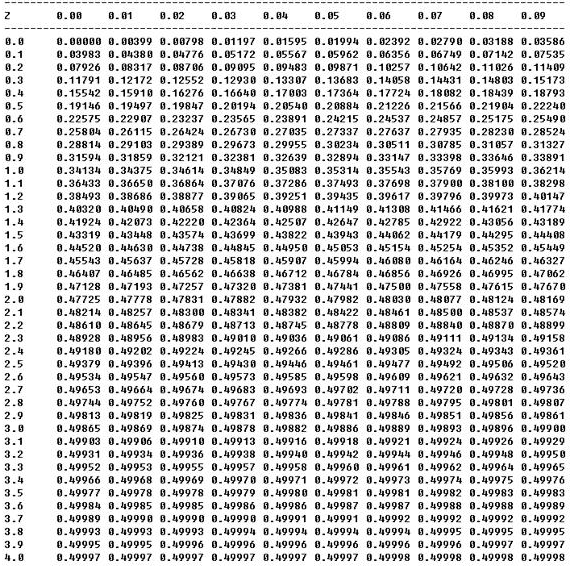
표준정규분포표 보는법
표준정규분표포의 가로 및 세로축은 우리가 원하는 z값을 나타낸다. 세로축(index)은 z값을 소수 첫째 자리까지 나타내었으며, 소수 둘째자리(header)는 가로축에 나타나 있다. 그리고 표 안에는 그 z값에 해당하는 확률, 즉 P(0<Z<z) 값이 적혀있다.
표준정규분포표를 활용하여 확률구하는 방법
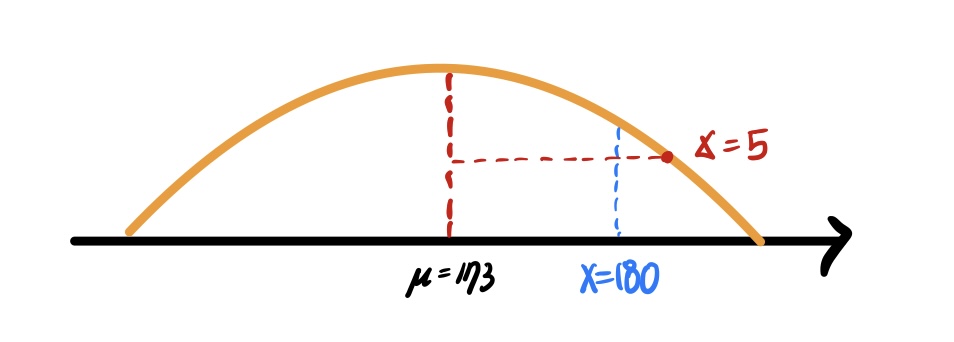
예) 대한민국 남성의 평균 키는 173cm이다. X는 키가 180cm라고 했을 때, 대한민국 내에서 상위 몇%라고 할 수 있는지 확률을 구하라.
( 표준편차는 5라고 가정한다. )
Z = (X - μ) / σ
= (180 - 173) / 5
= 7 / 5
= 1.4
∴ Z = 1.4
이 그래프가 표준정규분포라면
밑넓이 = 1
평균 = 0
표준편차 = 1 이다.
(이전 포스팅 (2) 조건간 차이검증 방법, 데이터 추론 참고)
위 표준정규분포표를 보며 Z값을 구할 수 있다.
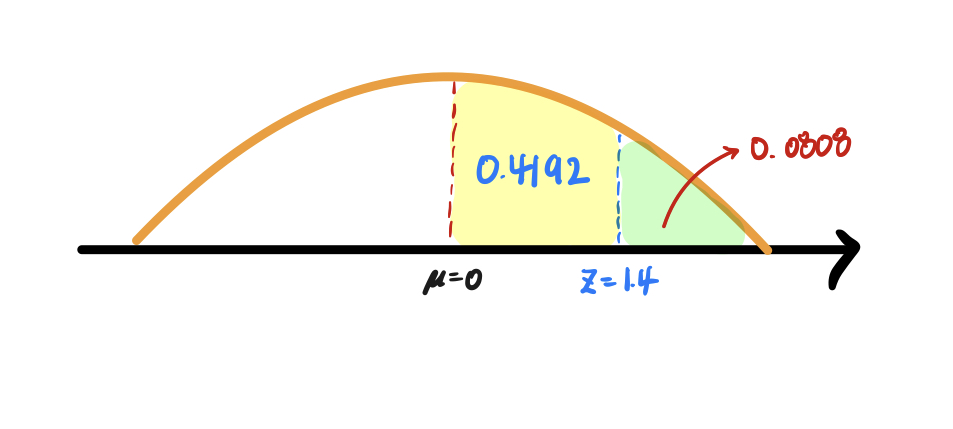
index = 1.4
header = 0.0
μ = 0 ~ Z = 1.4 까지의 밑넓이는 0.4192 이다.
밑넓이가 1일 때 0 이상의 밑넓이는 0.5이니
0.5 - 0.4192 = 0.0808 임을 구할 수 있다.
00808 * 100 = 8 이므로
X의 키인 180cm는 대한민국의 상위 8%에 해당하는 것을 구할 수 있다.
6sigma
표준정규분포표를 이용해서 특정 확률을 이루는 z의 구간을 구해낼 수 있다.
z의 절대값이 커진다는 것은 영역이 좁아진다는 의미이며 이는 영역의 확률이 줄어든다는 뜻이다. 즉, 엄청 낮은 불량률을 나타낸다.
0가설검정
나의 추론과 반대되는 추론이 참일 확률을 계산하는 것이다.
0가설이 참일 확률이 높은가, 낮은가를 따지는 것이며,
0가설 참일 확률 낮다 -> 반대추론이 참일 확률 낮다 -> 내 추론이 맞다 는 결론을 도출할 수 있다.
추론이란, 내 추론의 정확성을 따지며 내가 틀릴 확률을 따져서 계산하는 것이다.
0가설과 대립가설
- 나의 추론과 반대되는 추론이 참이 될 확률 계산하는 가설
- 나의 추론과 반대되는 추론 : 0가설
- 나의 추론 : 대립가설
그렇다면 몇%가 나와야 높은 확률로 볼 수 있는가?
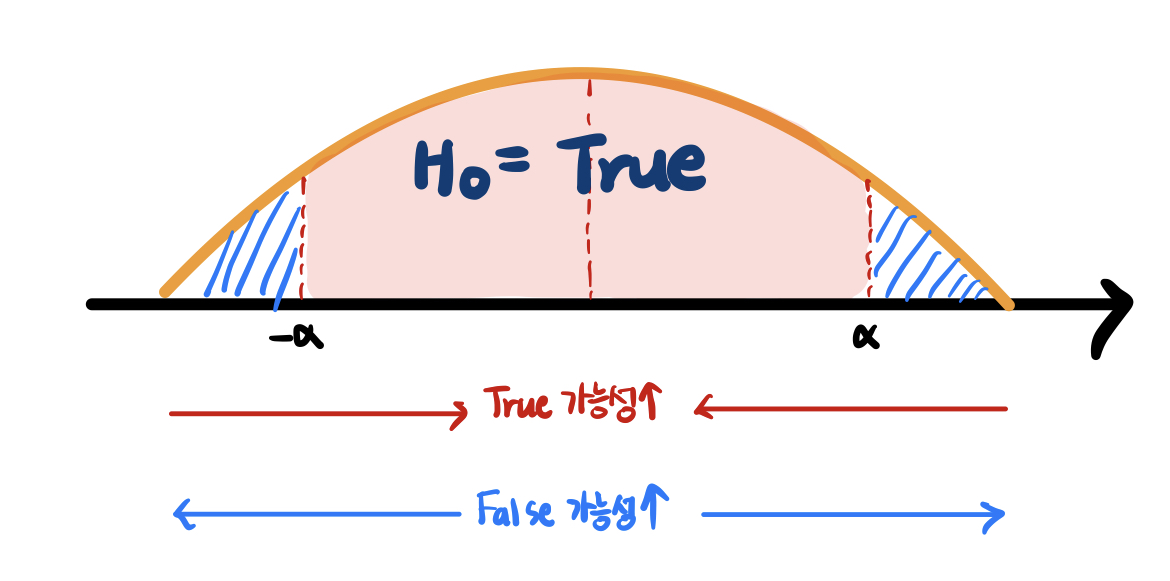
0가설검정은 통계적 추론을 위해서 0가설이 참일 확률과 그 확률의 기준선이 필요하다.
그 기준선을 α라고 하며 통상적으로 5%로 나타난다. 즉 5%보다 낮으면 낮은 확률로 본다.
실제 샘플데이터를 기반으로 0가설이 참일 확률을 구하는 것을 p-value라고 하며,
α > p : 0가설 기각 -> 내 추론이 맞음
α < p : 0가설 기각 불가 -> 내 추론은 ‘통계적으로 근거가 없음’으로 판단
0가설검정 구하는 방법
예) 까마귀 100마리를 샘플링하였다. "까마귀는 까맣다"는 사실이 참일 확률은 ?
0가설 : 까마귀는 까맣지 않다.
만약 까마귀가 빨간색인 것이 100마리 중 4마리라면
4 / 100 = 0.04 이다. 즉, p-value = 0.04이다.
α = 0.05 , p-value = 0.04
α > p-value 이다. 즉 0가설은 기각되며
대립가설인 "까마귀는 까맣다"가 채택된다.
'Computer > Data' 카테고리의 다른 글
| 데이터 분석 기초 쌓기 (2) 조건간 차이검증 방법, 데이터 추론 (0) | 2021.01.06 |
|---|---|
| 데이터 분석 기초 쌓기 (1) 기본 통계 지식 (0) | 2021.01.06 |
- Total
- Today
- Yesterday
- 파이썬 오름차순 정렬
- 백준 별찍기
- 백준
- 코테준비
- 파이썬 거꾸로
- 파이썬 내림차순 정렬
- 리눅스계정
- 백준1942
- reversed함수
- range특징
- 파이썬 덧셈
- 백준2920
- 백준2440
- 코테
- 백준2441
- 별찍기 -1
- 파이썬 find
- 오른쪽정렬
- 백준2007년
- 파이썬 오른쪽정렬
- 리눅스계정경로
- 백준코테
- 파이썬 반복문
- 별찍기 -4
- 파이썬
- 코딩테스트
- 별찍기 -3
- 별찍기 -2
- 백준 2742
- 백준11721
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
